Demonstration 7
Sorting

Introduction

Demonstration 7 provided the practical component for Chapter 9: “Sorting” of my unpublished textbook on composing programs. It illustrates how sorting might be used both to prioritize options for a decision and to arrange elements within statistical frames. In addition, it addresses for the first time in these Demonstrations the very important compositional problem of coordinating multiple parts. It also addresses the equally important methodological problem of generating a composition in several stages of production.

Compositional Directives

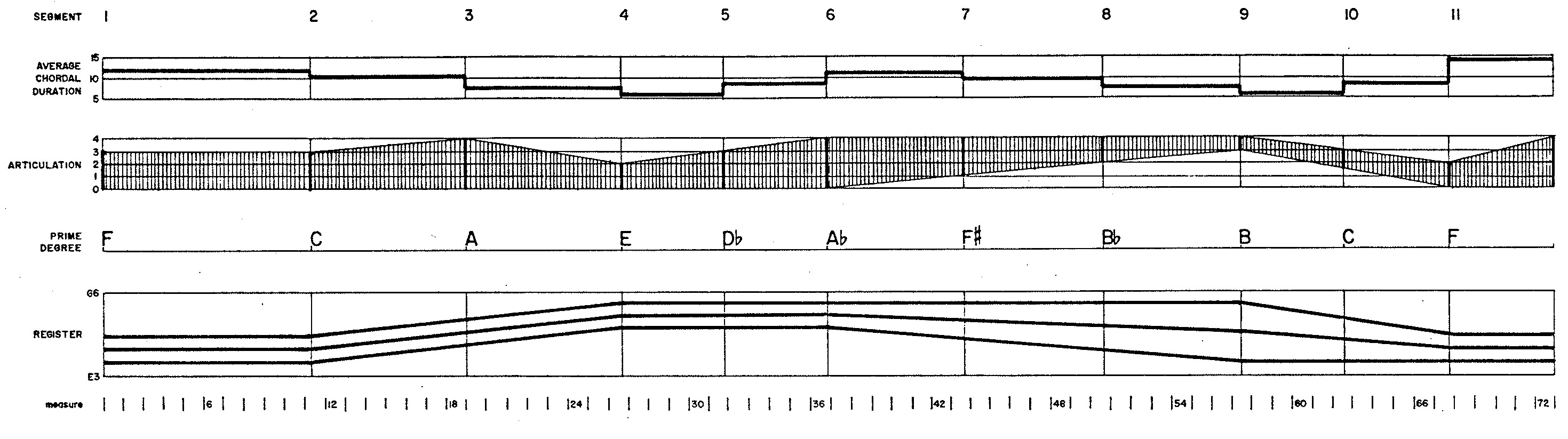
The musical structure of Demonstration 7 has three levels. At the global level, the piece as a while divides into eleven segments. At the median level, each segment divides in turn into from three to eight three-part chords. Owing to the monophonic nature of the clarinet, these chords must be arpeggiated as single notes; this last division of chords into notes comprises the local level of structure.

Figure 1 graphically presents the compositional data affecting the eleven segments. Each segment is characterized by an average chordal duration, an evolving range of values affecting the articulation of individual notes, by the ‘prime degree’ of an octatonic scale, and by evolving registers for each of the three parts in each chord. The graph of articulations indicate ranges of uniform randomness used to select between slurred, normal, and detached notes. The three bold contours on the registral graphs indicate central pitches around which the low, middle, and high chordal pitches are located.

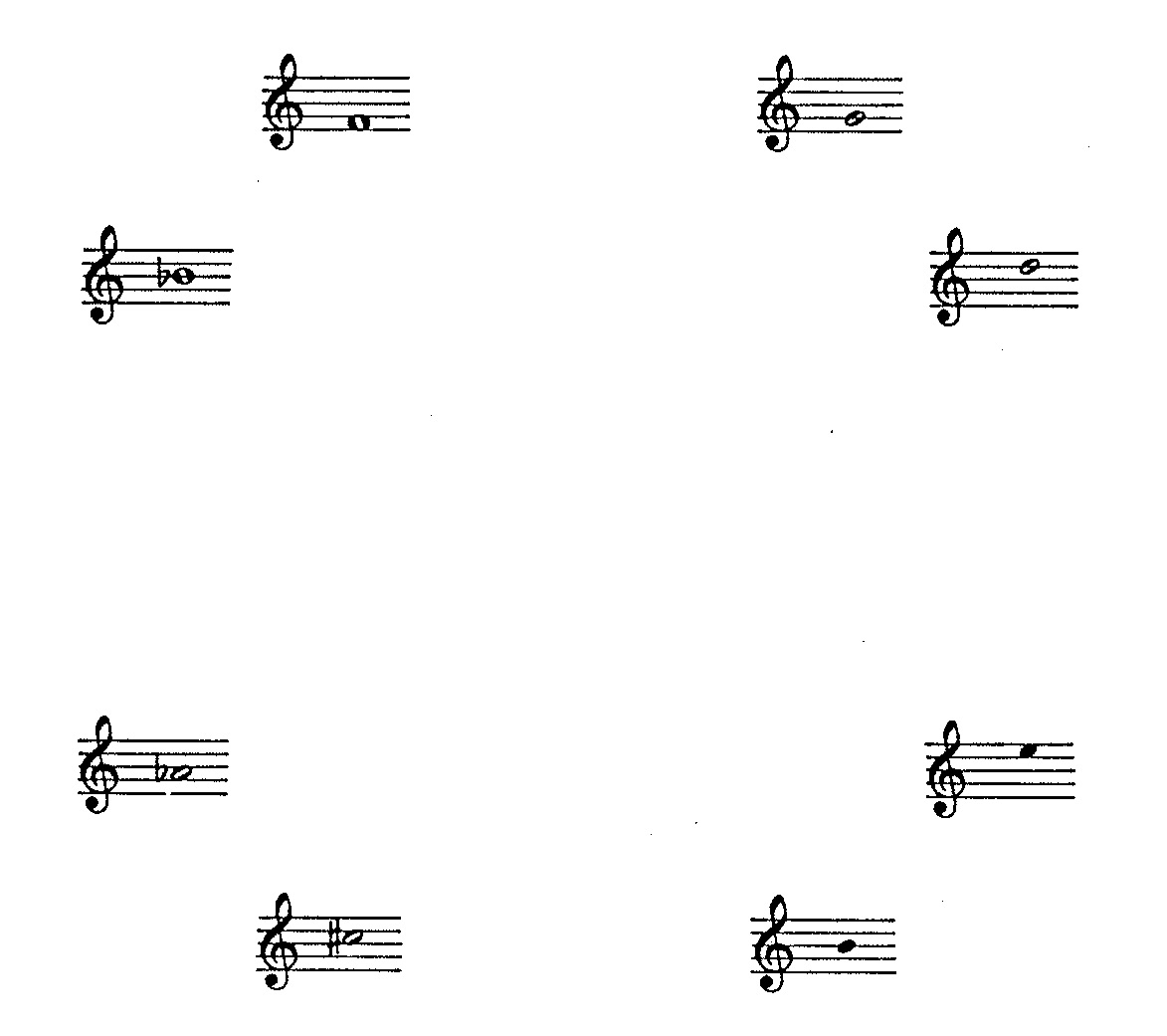
Of special significance to the global structure are the octatonic scales, which consist of alternating whole tones and semitones built above the “prime degree” specified for a segment. Figure 2 illustrates the relative weights allotted to each degree of the opening scale, which is built above the prime degree F. Whole-note heads in Figure 2 indicate heavily weighted degrees; half-note heads indicate moderately weighted degrees; solid noteheads indicate lightly weighted degrees. Thus the scale built on F most heavily emphasizes F and B! while suppressing (though not eliminating) the two degrees standing opposite on the circle of fifths: F# and B.

Similar weightings hold for the scales used in the remaining segments illustrated in Figure 3, which identifies prime degrees using the letter X and which identifies degrees shared in common using vertical lines. This scheme of weighting provides four effective ‘shades’ for each of the three octatonic scales recognized (reasoning from degree content alone) by conventional musical theory. It also provides two standards of distance between scales. Thus scales built on the prime degrees F and C, for example, may be regraded as close because they emphasize close regions of the circle of fifths. Alternately, scales built on the prime degrees F and B may be regarded as close because these two scales share the same collection of degrees.

The distribution of scale steps is flexible in that it does no great harm to choose a statistically inferior step for a specific part in a given chord, so long as the program can compensate for this choice in later decisions. For this reason, statistical considerations assume the least significance (in the technical sense) among the directives governing what pitches occur in a chord and governing how one chord progresses to the next. By contrast, the greatest significance is allotted to the least flexible considerations, the stylistic constraints.

The following constraints affect every part in every chord:

• No two pitches in a chord may form a unison, minor second, or major seventh. Neither may any two pitches form one of the three preceding intervals expanded by one or more octaves.
• A part may leap by an octave, but otherwise may not leap by more than a major sixth.
• No two parts may cross either explicitly within a chord or virtually between two consecutive chords.
• No two parts may move in parallel perfect consonances; neither may entire chords move in parallel, regardless of their constituent intervals.

The constraints just enumerated were formulated specifically for Demonstration 7. Whether you agree with them or not doesn't matter. What matters is your understanding of how to go about implementing such constraints so that a composing program can enforce them.

Figure 4 depicts the repertory of acceptable chords (nonblank cells) along with melodic ‘tendencies’ associated with each chordal type. Whole-note heads signify ‘stable’ pitches; solid noteheads signify ‘unstable’ pitches with tendencies in the directions indicated by arrows. These tendencies reflect traditional (19th century) attitudes toward the resolution of leading tones, dissonances, and unstable consonances; in cases such as diminished and augmented triads where a sonority admits to multiple tendencies, the author has selected one resolution arbitrarily. The tendencies occupy a level of significance below that of the constraints but above the statistical considerations inherent in the scales; resolutions are provided only when all of the constraints are satisfied. In deciding which parts of a chord should be composed in what order, the composing program gives first attention to parts with downward tendencies and next attention to parts with upward tendencies; only when all tendencies have been addressed are the ‘stable’ parts considered.

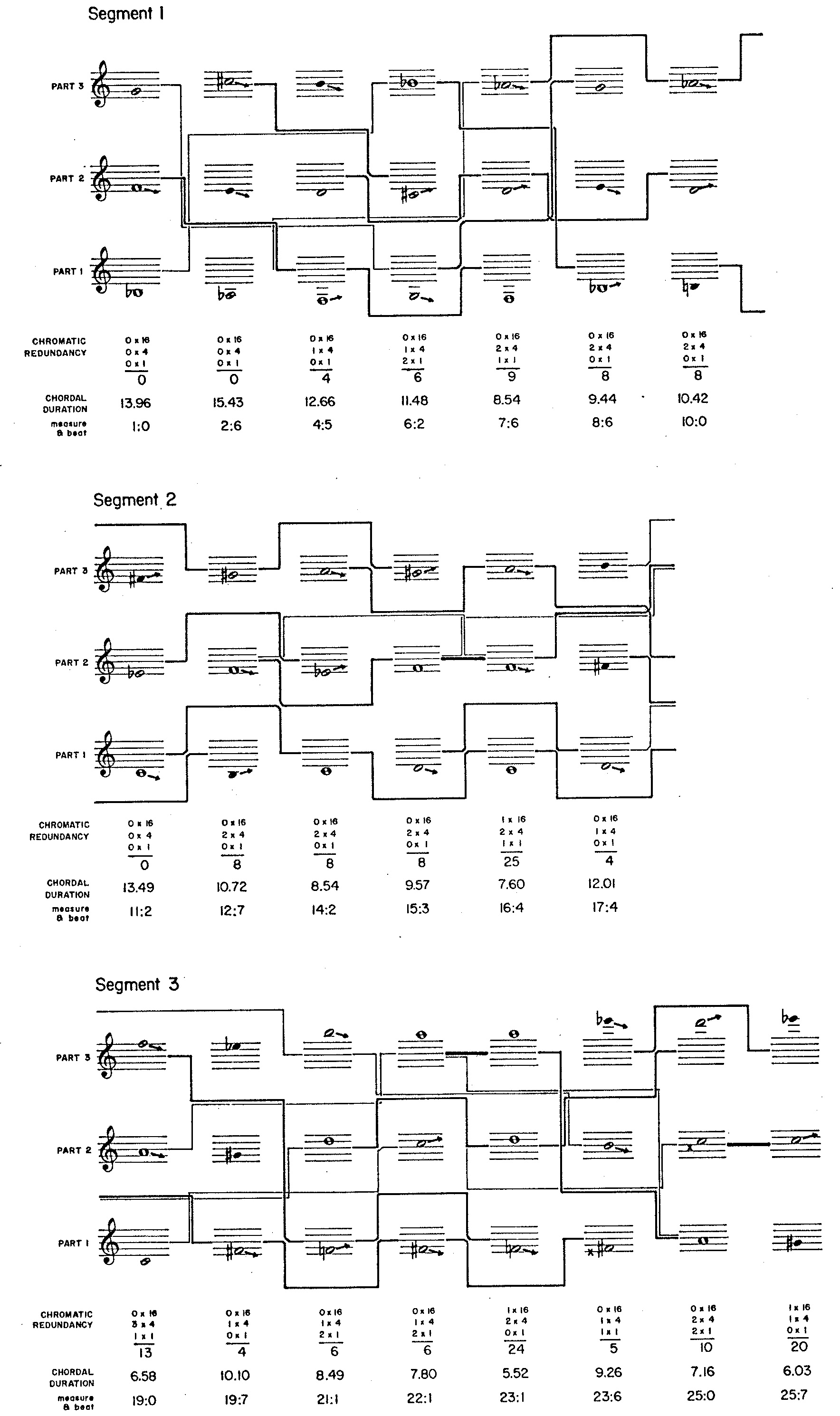
Figure 5 depicts the progression of chords selected for segments 1-3. Noteheads reflect the weightings indicated in Figure 4. Arrows following noteheads indicate tendencies derived from the matrix illustrated in Figure 4. X's preceding noteheads indicate failures to resolve tendencies inherent in the previous chord. The network of bold, medium, and thin lines shows relationships by common chromatic degrees in consecutive chords (bold lines) and chords separated by one or two intervening chords (medium and thin lines). Notice that unresolved tendencies are most prevalent in segment 3, where the upward evolution in register conflicts with downward trends propagated by successive downward tendencies.

A second item of concern at the median level of structure is the duration occupied by a chord. With respect to chordal durations, the composing program treats each segment of Demonstration 7 as a statistical frame. Each pool of durations adheres to John Myhill's generalization of the negative exponential distribution. The distribution parameters are the average chordal durations indicated in Figure 1 and a fixed proportion of 2.0 relating minimum to maximum durations. The program sorts these durations so that the longest durations in a segment go to those chords sharing the fewest chromatic degrees in common with their immediate predecessors. In addition to depicting the chordal progression for the first three segments of Demonstration 7, Figure 5 illustrates how chordal durations depend upon common chromatic degrees.

The directives governing how the program arpeggiates chords include a proscription against repeating a pitch for two consecutive notes (leaps by one or more octaves are quite legal) and a rule requested by clarinettist James Perone which forbids downward slurs larger than an octave. Subject to these constraints, the program selects pitches heuristically with cumulative feedback from the current chord. This process acknowledges the ‘stable’ pitches in a chord by assigning them one-and-one-half times the weight assigned to pitches with melodic tendencies. At the beginning of each chord, the program resets all cumulative statistics to zero so that the first three notes in each each arpeggio will present all three chordal pitches.

The duration of any note in an arpeggio is a sixteenth; however, a note may be articulated in one of three modes: (a) slurred to successor, (b) normal, (c) detached from successor by sixteenth rest. The tactic for selecting articulations reflects the TENDENCY feature of Koenig's Project Two. To select an articulation, the program generates a random value uniformly within the evolving range depicted in Figure 1. Values between 0.0 and 1.0 produce slurred notes, values between 1.0 and 3.0 produce normal notes, and values between 3.0 and 4.0 produce detached notes.

The transcribed product appears in Figure 6.

Implementation

The following explanations seek to tease out the strands of code that affect particular attributes, and thus to illustrate multi-criteria heuristics in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.

The FORTRAN source code for program DEMO7 is reproduced in Listing 1 (a) and Listing 1 (b). This main program is responsible for realizing the global structure of Demonstration 7. Also within DEMO7's domain of responsibility is the role of controller for subroutines delegated with realizing the median and local structure. There are three such subroutines, corresponding to three stages of production:

• Stage I: Part Writing — Subroutine PARTS, reproduced in Listing 2, composes a chord. Line 71 of program DEMO7 makes a separate call to PARTS for each chord in each segment. PARTS has two ancillary subroutines: EVAL (Listing 3) and LEGAL Listing 4).
• Stage II: Chordal Durations — Subroutine CHDRHY, reproduced in Listing 5, completes the median structure by assigning a duration to each chord. Line 86 of program DEMO7 makes a separate call to CHDRHY for each segment.
• Stage III: Arpeggiation — Subroutine ARPEGG, reproduced in Listing 6, realizes the local design by arpeggiating each chord. Line 109 of program DEMO7 makes a separate call to ARPEGG for each chord in each segment.

Listing 1 (a): Program DEMO7, lines 1-78.		Listing 1 (b): Program DEMO7, lines 70-115.

Although DEMO7 consolidates these three stages under a single main program, in practice it is usually advantageous to implement successive stages of production as independent programs linked through files of intermediate products, which files reside on a mass-storage device. This enhancement has been dispensed with here for reasons of brevity; it would have required the programs implementing each stage to include features for reading the products of earlier stages from one or more old files for further processing along with additional features for writing the products of the current stage out to a new file.

Lines 17-24 of DEMO7 proper specify the musical attributes characterizing each segment of Demonstration 7, as depicted in Figure 1. The declaration of parameter MSEG in line 5 fixes the number of segments at 11. The program organizes attributes into arrays identified by the following symbolic abbreviations:

• The average chordal durations shown in the topmost graph of Figure 1 were derived by dividing segment durations into chord counts. Array DURSEG, initialized in line 20, specifies segment durations in sixteenths. Array CHDSEG, initialized in line 20, specifies chord counts for each segment. DEMO07 dereferences CHDSEG(ISEG) in line 60 preparatory to calling subroutine DEMO07, in line 84 preparatory to calling subroutine CHDRHY, and in line 97 preparatory to calling subroutine ARPEGG. At each of these places the common variable ICHD indexes the chord position from the beginning of the piece.
• The second-from-top graph in Figure 1 plots articulations as an evolving sub-region of uniform probability which is contained within the range from 0 to 4. The same data comes into program DEMO7 through array ARTSEG. This 2×MSEG array is initialized in line 23. Each array element expresses an Array element ARTSEG(1,ISEG) gives the lower limit of this sub-region during segment number ISEG, while array element ARTSEG(2,ISEG) gives the upper limit during the same segment. Lines 100-103 of program DEMO07 dereference segment-boundary articulations from ARTSEG into the simple variables BEGALW, ENDALW, BEGALW, and ENDALW, which are passed as arguments to subroutine ARPEGG.
• The third-from-top portion of Figure 1 lists primary degrees for octatonic scales. Variable names pertaining to primary scale degrees are identified by the abbreviation PRM, while Thus array PRMSEG, initialized in line 15, specifies primary degrees for segments.
• The fourth-from-top graph in Figure 1 plots registers for each of three parts. Each register locates the bottom pitch of a one-octave gamut. The same data comes into program DEMO7 through array REGSEG. This 2×MSEG array is initialized in line 21. Array element REGSEG(1,ISEG) gives the register for the lowest part during segment number ISEG. Array element REGSEG(2,ISEG) gives the register for the highest part during the same segment.

Part Writing

Stage I treats composing the progression of chords as a problem in three-part, note-against note counterpoint. More precisely, Stage I takes as input the compositional directives depicted in Figure 1, Figure 2, Figure 3, and Figure 4. As output, Stage I selects a pitch for each part within each chord. This output is itemized by Figure 5 for segments 1-3 of Demonstration 7.

Pitch selections in Stage I conflate separate selections of two musical attributes, register and scale step.

Registers

The register-by-part array REGPRT is populated by program DEMO07 and consumed by subroutine PARTS. Common memory declarations in line 7 of DEMO07 and in line 14 of PARTS render REGPRT accessible to both program modules. The populating step happens in lines 65-69 of program DEMO07, which use the segment-boundary registers from REGSEG to calculate chord-specific and part-specific values for REGPRT. This happens just before the call to PARTS happens in line 72. The interpolation factor X proceeds from zero (line 61) to unity by equal increments (line 62) over the span of a segment. The lowest-part register as of X is calculated by a call to the library function EVLIN in line 65 and stored in the simple variable RLOW; line 67 rounds this value to an integer and saves the resulting low-part register in array element REGPRT(1). The highest-part register as of X is calculated likewise in line 66 and stored in the simple variable RHGH; line 69 rounds this value to an integer and saves the resulting high-part register in array element REGPRT(3). The middle-part register REGPRT(2) is then calculated from the average of RLOW and RHGH.

Loop Structure

The FORTRAN source code for subroutine PARTS appears in Listing 2. The structure of subroutine PARTS is an outer part-enumerating loop spanning lines 33-50 which encloses an inner pitch-selection loop spanning line 39-45. Scale steps are selected using the method of cumulative feedback, but subject to constraints such as the interval combinations itemized in Figure 4.

• The scale-step selecting mechanism within subroutine PARTS begins with a call to subroutine EVAL in line 37. EVAL populates two arrays, a scale-degree scheduling array SCDSCL and a pitch-conversion array PCHSCL. (You'll learn how momentarily.)
• The loop spanning lines 39-45 considers each scale step ISCL in the order prescribed by SCDSCL.
• After dereferencing ISCL, the loop decodes the the candidate pitch IPCH from PCHSCL and the interval ITVL from the previous pitch for the current part, PCHPRT(IPRT,ICHD-1), to IPCH.
• The call to the logical function LEGAL assesses whether the ISCL satisfies all applicable constraints. If so, PARTS breaks out of the pitch-selecting loop.
• PARTS captures IPCH in PCHPRT(IPRT,ICHD). Two other aspects of the pitch are derived from IPCH: a chromatic degree (1-12) is captured in DEGPRT(IPRT,ICHD) while the octave above 32' C is captured in OCTPRT(IPRT,ICHD).

Stage I makes use of sorting in two places: Subroutine PARTS's call in line 31 to the library subroutine LSORT determines the order of parts by which pitch selection will proceed. Within subroutine EVAL, lines 62-79 implement a double-keyed sort which determines the order by which scale steps will be considered for selection. The order of parts strongly influences pitch selection, since a pitch chosen for one part limits the choices available to the others. However the outcome of pitch selection for one chord strongly influences the order of parts in the next chord, owing to the tendencies itemized in Figure 4.

Part Scheduling

The declarations of parameter MPRT in line 5 of DEMO07 and again in line 5 of PARTS fix the number of parts at 3. Notice that the parts are not enumerated in part-number order. Rather, the loop index IDXPRT determines the current part IPRT via the scheduling array SCDPRT. This scheduling array contains the part numbers 1, 2, and 3.

First thing into subroutine PARTS, line 30 calls the library subroutine SHUFLE to randomize the order of SCDPRT. This step eliminates any bias implicit in how part numbers are enumerated. Line 31's call to LSORT reschedules part numbers according to tendencies stored for part #1 in array element TNDPRT(1,ICHD-1), for part #2 in array element TNDPRT(2,ICHD-1), and for part #3 in array element TNDPRT(3,ICHD-1). (Remember that FORTRAN passes subroutine arguments by address rather than by value.) Each TNDPRT element has one of the following values: (2) downward tendency, (1) upward tendency, and (0) no tendency — these are the values packed into the ones, tens, and hundreds digits of array TNDTVL during this array's initialization in lines 17-27. In the event that multiple parts have tendencies of the same urgency, line 30's shuffling provides the tie breaker.

To understand how array elements TNDPRT(1,ICHD-1), TNDPRT(1,ICHD-1), and TNDPRT(1,ICHD-1) were populated with values from array TNDTVL, we need to skip backward in process-time to the previous chord (by decrementing ICHD) and skip forward past the part-enumerating loop to line 52 of subroutine PARTS. At this point in the process, array element PCHPRT(1,ICHD) holds the pitch selected for part #1, PCHPRT(2,ICHD) holds the pitch selected for part #2, and PCHPRT(3,ICHD) holds the pitch selected for part #3. Thus I1=MOD(PCHPRT(2,ICHD)-PCHPRT(1,ICHD),12) (see line 52) gives the chromatic interval between part #1 and part #2, which value is suitable for determining a row in Figure 4. Likewise I2=MOD(PCHPRT(3,ICHD)-PCHPRT(2,ICHD),12) (see line 53) gives the chromatic interval between part #2 and part #3, which value is suitable for determining a row in Figure 4. Line 54's call to the library subroutine UNPACK extracts the hundreds digit of TNDTVL(I2,I1) into TNDPRT(1,ICHD), the tens digit of TNDTVL(I2,I1) into TNDPRT(2,ICHD), and the ones digit of TNDTVL(I2,I1) into TNDPRT(3,ICHD).

Thus can heuristic methods positively influence the order in which decisions are taken. Very few pitches (possibly only one) will be available to resolve a particular downward tendency, so performance is improved when contentions with other parts are minimized.

Scale Statistics

We now tease out the programming strand which maintains cumulative statistics for scale steps.

• The statistical strand reaches up to the main program DEMO07. The declaration of parameter MSCL in line 5 fixes the number of scale steps at 8; this parameter sizes arrays SCALE, EMPH, and CUMSCL. The statement populating array SCALE in line 15 lists the chromatic displacements (alternating whole and half steps) needed to form an octatonic scale above a primary, while the statement populating array EMPH in line 16 details the weights corresponding to each scale step, as pictured in Figure 2. Array CUMSCL tracks scale-degree usage through the whole of Demonstration 7.
• Lines 48-57 initiate the segment-enumerating loop of program DEMO07. This particular code section configures the octatonic scale which will come into effect during the segment, and the object is to align things so the statistics compiled in one segment pass along from one scale step in one segment to another scale step in the next segment following the pathways shown in Figure 3. That is, statistics are handed of either to common scale steps or to nearby cross relations. This exchange is facilitated by array FNCSEG, which is initialized in line 16. FNCSEG identifies which scale step number will be associated with each segment's primary degree. Thus for segment #2, the prime degree IPRM is C% and the associated scale step number LSCL will be FNCSEG(2), which is 6. Thus array element CUMSCL(6), which tracked usage for C# in segment #1, will now track usage for C% in segment #2.
• The loop spanning lines 50-57 fleshes out information for each of the octatonic scale steps, taking account the offset from FNCSEG. Array DEGSCL is populated with chromatic numbers (1-12) calculated as IPRM+SCALE(ISCL) and wrapped around when necessary into the range from 1-12. Array WGTSCL is populated with weights drawn from array EMPH. Array CUMSCL is biased forward in line 55 so that the first pitch selection in the segment will better reflect the weights in WGTSCL. This third action is reversed in lines 75-77, after Stage I pitch selection has completed for the current segment.
• The statistical strand continues within subroutine EVAL. EVAL responds to a call from subroutine PARTS just before entering the latter's pitch-selection loop. Here the only reference to array CUMSCL happens within the SCDSCL sort implemented by lines 62-79, and this sort treats CUMSCL values as secondary criteria. Array RESSCL provides the primary criteria; the values in RESSCL being integers ranging from 0 to 3. However, these values are grainy enough to allow CUMSCL to exert substantial influence.
• The final action of the statistical strand is line 49 of subroutine PARTS. After selecting scale step ISCL in the preceding loop, this subroutine increments CUMSCL by 1.0/WGTSCL(ISCL).

Listing 3: Subroutine EVAL.		Listing 4: Subroutine LEGAL.

Resolutions

So much for cumulative statistics. What of those other criteria the RESSCL values which supersede CUMSCL in deciding which scale steps should first be considered?

Array TNDTVL stores the tendencies depicted in Figure 4 in the form of three decimal digits indicating tendencies for the low, middle, and high parts, respectively. The interval between the low and middle pitches determines the row of TNDTVL, while the interval between the middle and high pitches determines the column. Null entries in TNDTVL correspond to unacceptable chordal types. The digits 0, 1, and 2 have the following meaning:

0. Stable pitch; no urgency.
1. Upward tendency (leading tone); low urgency.
2. Downward tendency (dissonance or unstable consonance); high urgency.

Subroutine PARTS determines pitches by drawing chromatic degrees from array DEGSCL and locating these degrees in the octave determined by array element REGPRT(IPRT). Both degrees and registers are determined by the main program from the compositional data depicted in Figure 1. If a tendency is in force, then EVAL rates each pitch with an integer from 0 (no potential for resolving this tendency) to 3 (high potential). Line 55 of EVAL stores this rating in array RESSCL. Notice that EVAL considers lack of motion or stepwise motion in the ‘wrong’ direction preferable to leaps, in the event that an orthodox resolution proves infeasible. Notice also that EVAL treats upward and downward tendencies dissimilarly. When a part has an upward tendency, EVAL prefers upward steps, unisons, and then downward steps (lines 31-39). When the part has a downward tendency, EVAL prefers downward steps as expected but otherwise prefers upward steps to unisons.

The ratings stored in array RESSCL for each of the eight pitches along with the statistics accumulated in array CUMSCL provide more significant and less significant values, respectively, which PARTS uses to compile a schedule of preferences. PARTS then steps through this schedule, consulting the logical function LEGAL in order to determine if a scheduled pitch adheres to all stylistic constraints. The first pitch accepted by LEGAL concludes the process of selection²; it only remains for PARTS to store this selection (lines 46-48) and to update the appropriate element of CUMSCL (line 49) so that future decisions will be more inclined to favor other scale steps.

Constraints

The logical function LEGAL enforces the four constraints listed previously among the compositional directives. The FORTRAN source code appears as Listing 5. Among the variables shared through common memory are

• ICHD, the current chord number from program DEMO07.
• IPRT, the current part number assigned in line 34 of subroutine PARTS.

Of the function arguments,

• IDXPRT is the current part index from the loop starting in line 33 of subroutine PARTS,
• SCDPRT is the part-scheduling array whose contents were ordered by lines 30-31 of subroutine PARTS,
• IPCH holds the candidate pitch expressed in semitones above 32' C, assigned in line 41 of subroutine PARTS, and
• ITVL is the distance to IPCH in semitones from the corresponding pitch in the previous chord assigned in line 42 of subroutine PARTS.

Having IDXPRT and SCDPRT enables LEGAL to enumerate those parts for which pitches have already been selected for chord number ICHD. This is done by ranging a secondary index LDXPRT from 1 to IDXPRT-1 (line 32), by dereferencing LPRT=SCDPRT(LDXPRT) (line 33), and then dereferencing LPCH=PCHPRT(LPRT,ICHD) and LPCH1=PCHPRT(LPRT,ICHD-1). These computations allow LEGAL to undertake the inter-part comparisons needed to enforce the various pitch constraints.

It often happened that no scheduled pitch satisfied all constraints. Indeed, the author found after running DEMO7 with 20 different random seeds, only 6 runs terminated successfully, for a failure rate of 70%! Methods of recovering from such failures and of ensuring more reliable performance are examined in connection with Demonstration #11

Chordal Rhythm

Stage II of production for Demonstration 7 is implemented by subroutine CHDRHY, for which the source code may be found in Listing 5. Of the three subroutine arguments, KCHD holds the number of chords in the current segment, AVG holds the average chordal duration from the topmost graph in Figure 1, and PROPOR holds the ratio of maximum to minimum durations. This latter argument is throttled down to a consistent value of 2.0. The common memory variable ICHD holds an index to the first chord in the segment.

The loop spanning line 20-41 of CHDRHY does two things:

• It populates the scheduling array CHDTMP with the position of each chord in the current segment.
• It populates the IDXCHDth element of the packed key array CHMCHD with a value quantifying the chromatic redundancy of the IDXCHDth chord in this segment.

After exiting from the loop, four additional steps are required:

• Line 44 calls the library subroutine SHUFLE to randomize the scheduling array CHDTMP. This step eliminates any influence by chord order, should two chords share the same measure of chromatic redundancy.
• Line 45 calls the library subroutine ISORT to arrange the chord positions of CHDTMP into increasing order of CHMCHD values.
• Line 47 calls the library subroutine FILLX to populate array DURTMP with a pool of durations in descending order, which pool conforms to the average duration AVG and the max/min proportion PROPOR.
• The loop spanning lines 48-50 distributes the durations in DURTMP to chords in the order scheduled by CHDTMP.

The measure of chromatic redundancy computed in lines 20-41 is in fact a packed key of the form:

L  =

ΣN n=1

k(m,n)×BN-n

Where k(m,1),k(m,2),…,k(m,N) are numeric criteria sorted into order of significance. By ‘order of significance’ I mean that a difference between k(m₁,n) and k(m₂,n) is meaningful only if there is no difference between k(m₁,1) and k(m₂,1), between k(m₁,2) and k(m₂,2), and so forth all the way through k(m₁,n-1) and k(m₂,n-1).

The base of exponentiation B is calculated as:

B  =  1 +

max M m=1

[

max N n=1

k(m,n)

]

For this application the chord size is MPRT=3, so the maximum number of common tones shared between two chords is also 3. Thus B = MPRT+1 in line 25.

Arpeggiation

Stage III of production for Demonstration 7 is implemented by subroutine ARPEGG, for which the source code may be found in Listing 6. ARPEGG consists of a note-composing loop (lines 21-65) which iterates as many times as necessary to fill out the duration of a chord. Each iteration of the note-composing loop divides into two tasks: part selection and articulation.

Arguments for subroutine ARPEGG are all concerned with articulation. Other pertinent information comes in through common memory: ITIME is the current time in sixteenth notes from the beginning of the piece, which value is incremented within subroutine
WNOTE, called in lines 52, 60, and 63. (This particular
WNOTE is a variation of the one originally presented for Demonstration 1.) ITIME advances with each loop iteration until it reaches KTIME, the chord-ending time, whose value was assigned in line 108 of program DEMO07. The current chord number comes down from DEMO07 to ARPEGG through the common variable ICHD.

Part Selection

Lines 24-52 select one of the three parts in the chord to provide a pitch for the note. The tactic is heuristic with cumulative feedback and is reminiscent of the method used to select chromatic degrees for Demonstration 6.

1. Part numbers are accessed indirectly through the scheduling array SCDPRT, which is populated in line 16. Statistics of cumulative usage are maintained for each part in array CUMPRT.
2. Line 24's call to the library routine SHUFLE prevents favoring lower-numbered parts when usage statistics come into balance.
3. Within the part-selecting loop spanning lines 28-42, the first statement uses SCDPRT to dereference the candidate part LPRT from the loop index IDXPRT.
4. The inner loop spanning lines 31-42 serves to identify the part number IPRT which satisfies both constraints (no part-repetition and no large downward slurs) and for which the cumulative usage CUMPRT(IPRT) is otherwise minimal.
5. Once a part IPRT has been selected, its cumulative-usage statistic must be updated. This happens in line 46-50. Notice that the increment depends upon TNDPRT(IPRT,ICHD). If TNDPRT(IPRT,ICHD) = 0, then the part is functionally stable and the increment is 1.0. If TNDPRT(IPRT,ICHD) > 0, then the part is functionally unstable and the increment is 1.5. Smaller increments mean larger weights and thus greater frequency of selection.

Articulation

Lines 54-64 select an articulation. The tactic follows the TENDENCY feature of Koenig's Project Two and reprises the approach taken for articulation in Demonstration 6.

1. An interpolation factor F is calculated relative to ITIME by line 54's call to the library function FACTOR.
2. The lower bound of the articulation range as of ITIME is calculated by a call to the library function EVLIN in line 55 and stored in the simple variable AHGH. The higher bound of the articulation range as of ITIME is calculated likewise in line 56 and stored in the simple variable AHGH. The middle-part register ARTPRT(2) is then calculated from the average of RLOW and AHGH.
3. Line 57 selects the mode of articulation IART by the expression IFIX(UNIFRM(ALOW,AHGH))+1.

In selecting parts, it sometimes happens that the constraint against large downward slurs could not be accommodated by the heuristic technique; in such cases the program ignored this constraint. The author then exercised editorial prerogative to remove the slur.

Packing and Unpacking

The library subroutines PACK and UNPACK³ implement conversion between packed and unpacked keys. PACK compresses an array of unpacked keys into a single variable. Its counterpart, UNPACK, dismantles a packed key into components. Both subroutines require four arguments:

1. VAR — Packed key (destination for PACK, source for UNPACK). VAR must be a simple integer variable in the calling program.
2. ARRAY — Array of unpacked keys (source for PACK, destination for UNPACK). ARRAY must be an integer array whose dimension in the calling program is NSIG (argument #4 below).
3. BASE — Base of exponentiation.
4. NSIG — Number of unpacked keys (levels of significance). NSIG must be a positive integer in the calling program.

Subroutine PACK applies the packed-key formula to the values in ARRAY, placing results in ARRAY. Subroutine UNPACK iteratively strips out leftmost component of VAL and places the component in the next available ARRAY element.

Sorting by Indirect Key

The library subroutines ISORT, LSORT, ASORT, and DSORT⁴ each sort a scheduling array based indirect key values stored in a second array. Calls to ISORT, LSORT, ASORT, or DSORT require three arguments:

1. SCHED — Schedule of index values. SCHED must be an integer array whose dimension in the calling program is NUM (argument #3 below). SCHED must contain the index values 1, 2, … NUM. Coming into the subroutine, these index values may be arranged in any order.
2. KEY — Array of key values, one for each index in array SCHED. KEY must be an array whose dimension in the calling program is NUM. ISORT and LSORT require KEY to be an integer array; ASORT and DSORT require KEY to be a real array.
3. NUM — Number of index values. NUM must be an integer in the calling program.

Subroutines ISORT and ASORT sort the SCHED values into ascending order of KEY values:

Modular Arithmetic

My library subroutine MOD implements modular arithmetic adjusted to the FORTRAN counting scheme. Calls to MOD require two arguments:

1. I — An integer value.
2. M — Modulus, must be a positive integer.

My implementation of MOD library subroutine follows the FORTRAN counting scheme by wrapping integers in the range from 1 to M. For examples, MOD(1,12) yields 1, MOD(0,12) yields 12, and MOD(13,12) yields 1. Such range mapping is convenient when the results are intended to index FORTRAN arrays. Beyond that, my implementation treats negative arguments the way mathematicians (rather than computer scientists) expect. Thus MOD(-2,12) yields 10. This behavior differs from the modulo operation offered by most programming languages, whose output ranges from 0 to M-1 (usually good) but whose processing of negative arguments is symmetric around zero: MOD(-2,12) yields -2 (bad for chromatic math).

Sorting with Cumulative Feedback

The library subroutine FUZZY⁵ implements scheduling driven by cumulative feedback with random leavening. Calls to FUZZY require five arguments:

1. SCHED — Schedule of index values. SCHED must be an integer array whose dimension in the calling program is NUM (argument #5 below). SCHED must contain the index values 1, 2, … NUM. Coming into the subroutine, these index values may be arranged in any order.
2. CUM — Cumulative statistics reflecting how much each schedule index has previously been selected. CUM must be a real array whose dimension in the calling program is NUM.
3. FUZZ — Array for temporary storage of derived keys. CUM must be a real array whose dimension in the calling program is NUM.
4. OFFSET — Likelihood of selection associated with the most-used option.
5. NUM — Number of index values. NUM must be an integer in the calling program.

DO NOT USE THIS ALGORITHM! FUZZY first evaluates the maximum statistic in array CUM, saving this maximum in the variable CMAX. It then calculates keys dynamically by setting FUZZ(I)=RANF()*(CMAX-CUM(I)+2.0*OFFSET)/2.0. It completes by calling DSORT(SCHED,FUZZ,NUM).

Comments

1. blah.
2. blah, blah.
3. The source code for subroutines PACK and UNPACK is discussed in Automated Composition, Chapter 9, p. 9-10.
4. The source code for subroutine ISORT is presented in Automated Composition, Chapter 9, p. 9-5. The remaining subroutines are explained as variants of ISORT.
5. The subroutine is misnamed owing to an indirect and erroneous understanding of fuzzy logic. The source code for subroutine FUZZY is discussed in Automated Composition, Chapter 9, pp. 9-13 to 9-14. Be warned that this source code is bogus. The feedback mechanisms employed for these Demonstrations were reworked into the procedures described in “Statistics and Compositional Balance”.