Demonstration 5
Cumulative Feedback
Introduction
Demonstration 5 provided the practical component for Chapter 7: “Conditional Selection II — Cumulative Feedback” of my unpublished textbook on composing programs. It illustrates how cumulative feedback1 might be used in a composing program. It employs the structure of phrases and notes used in Demonstration 2 and Demonstration 3 with the enhancement that phrases in Demonstration 5 are distinguished not only by phrase lengths, average durations, articulations, and registers, but also by scales.
Compositional Directives
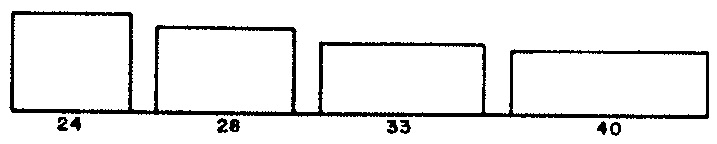
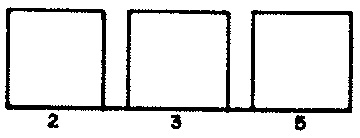
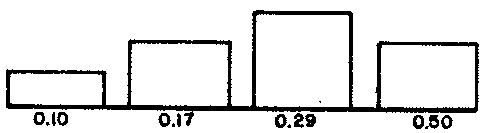
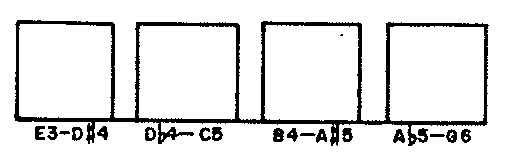
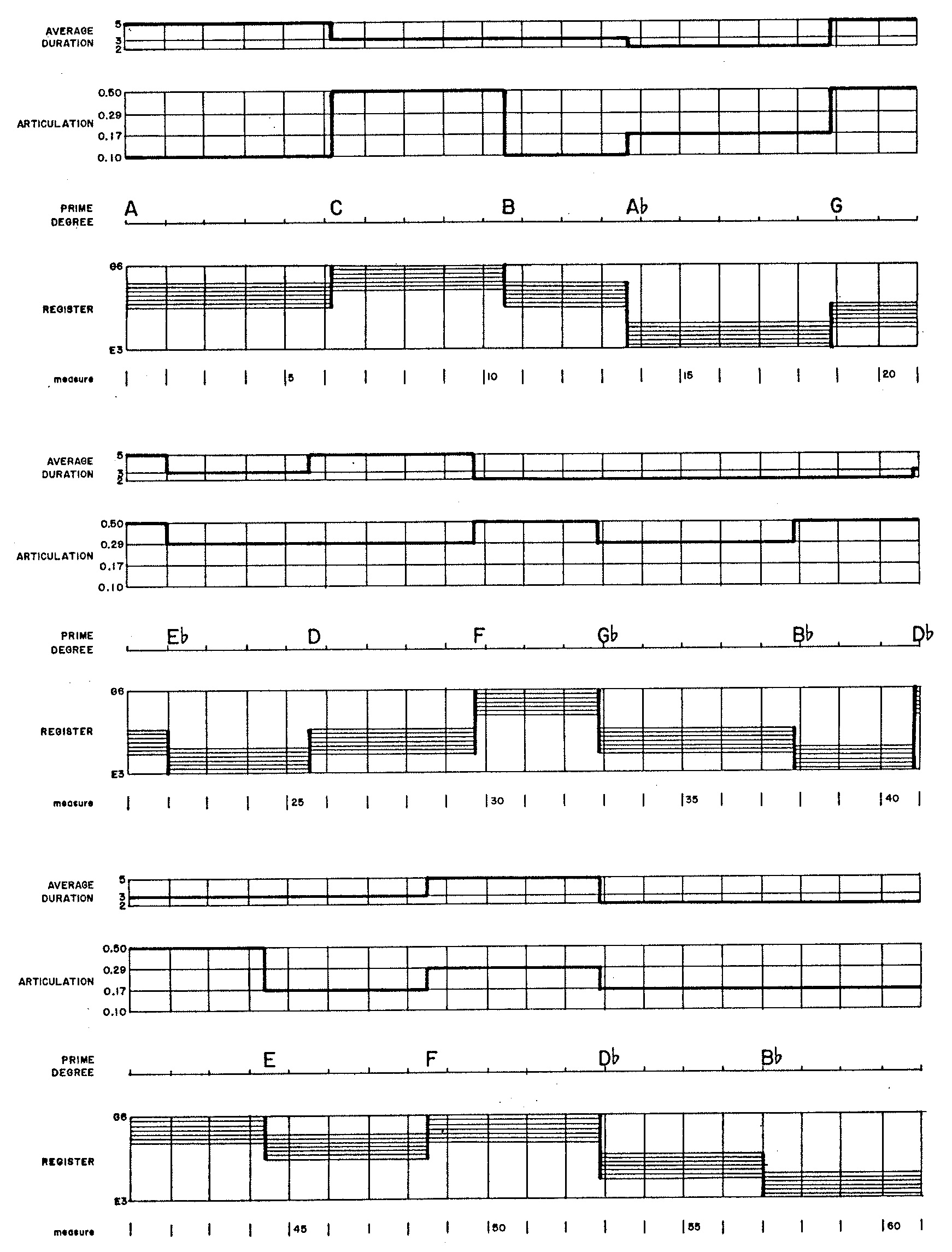
Attributes of phrases are selected using cumulative feedback in accordance with the statistical distributions depicted for phrase lengths in Figure 1 (a), for average note durations in Figure 1 (b), for articulations in Figure 1 (c), for prime scale degrees in Figure 1 (d), and for registers in Figure 1 (e).
Selection of phrase durations, average note durations, articulations, and registers is unconstrained. Selection of prime scale degrees is subject to two provisions:
- No two consecutive scales may share more than four common degrees, and
- No two consecutive primes may be related by a tritone.
Although the basic form of a scale corresponds to the Lydian mode, it is not used as such because the primary serves simply as an index for the program. There are no cadences or other means taken to establish these particular degrees as listener points of reference. For the purpose of Demonstration 5 it is most useful to think of the basic scale form as the collection of degrees generated by a sequence of six rising perfect fifths above the primary.
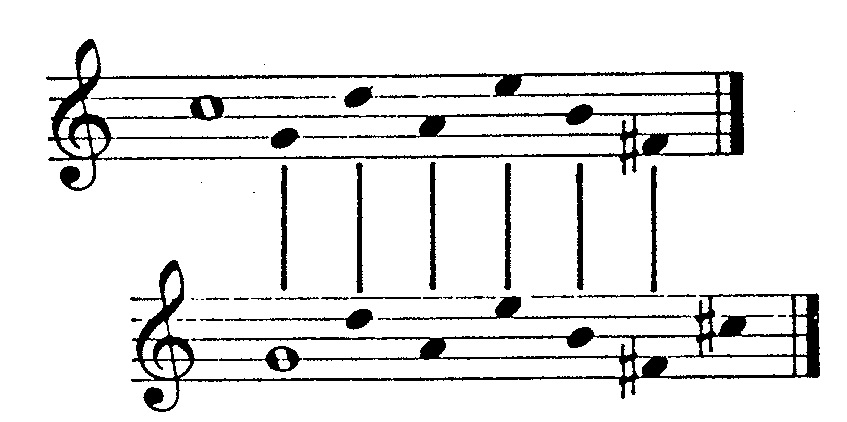
Contrast between individual transpositions of this basic form results from cross relations.2 The number of cross relations occurring between any pair of transpositions depends on the nearest distance between their primaries around the circle of fifths. For example, Figure 2 (a) shows that a scale starting on C has one cross relation and six common degrees with a scale starting on G. By contrast, Figure 2 (b) shows that a scale starting on C has four cross relations and three common degrees with a scale starting on E.
The prohibition against tritone-related primaries is pragmatic, motivated by the ambivalent common tones resulting when two scales have primaries related by a tritone. Notice in Figure 3 (a) how aligning the two F#'s throws C out of alignment with B#, while in Figure 3 (b) aligning C against B# throws the F#'s out.
|
|
|
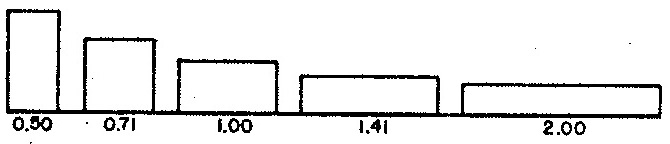
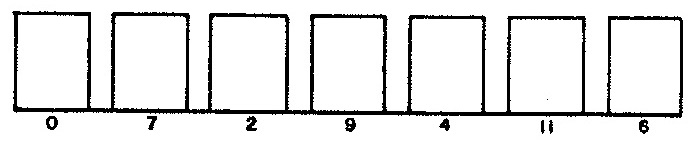
| Figure 4 (a): Distribution of note durations (relative to average note duration). | Figure 4 (b): Distribution of chromatic offsets from prime scale degree. |
Figure 4 (a) depicts the negative exponential distribution used to select durations for notes (rests last half as long), while Figure 4 (b) depicts the uniform distribution used to select degrees. The latter attribute is selected heuristically using cumulative feedback, with sensitivity to duration.
Degree selections are also constrained by the stylistic matrix depicted in Figure 5. This matrix rejects any two consecutive degrees related by a tritone, any three consecutive notes containing two identical degrees, and any three consecutive notes whose degrees make up dissonant triads of the forms C-C#-D, C-F#-B, or C-F-B, in any inversion, voicing, or transposition. The stylistic matrix works along with the intervallic relationships imposed by the scales — which each consist of seven adjacent positions on the circle of fifths — to establish a notably more consonant style than was apparent in Demonstration 4.
Matrices such as the one shown in Figure 5 provide one implementation tactic for enforcing constraints. Another tactic is the one advocated by Allen Forte in The Structure of Atonal Music, which is to compile a list of acceptable chord types in “normal form”, then validate each sequence of three degrees against the list. Still another tactic would be to formulate tests which directly implement the rules listed in the last paragraph. For example, there would be a test for tritones, another test for identities, a third test for triads of the form C-C#-D, and so forth. It happens the constraint matrix is the most efficient tactic of the three; however there is an up-front cost of enumerating all possible interval pairs and determining for each pair whether the sequence is stylistically acceptable or not.
Be reminded that these particular constraints apply to this particular Demonstration, and that electing these constraints here in no way binds us to impose the same constraints upon other projects.
Figure 6 graphs the musical attributes selected by the composing program for phrases.
Figure 7 Details the progression of scales and their linkages through common tones. Whole-note heads in Figure 7 signify ‘prime’ degrees; while vertical lines indicate degrees shared in common by consecutive scales.
A transcription of the musical product appears in Figure 8.
Implementation
The explanations to follow focus variously on five attributes of phrases and three attributes of notes. The purpose is to tease out the strands of code that affect a particular attribute, and thus to reveal the mechanics of cumulative feedback in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.
Program DEMO5 is reproduced in Figure 9 (a) while its corresponding subroutine
PHRASE Figure 9 (b).
Like programs DEMO2 and DEMO3,
DEMO5 reflects the musical structure through an ‘outer’ composing loop (lines 36-68 of DEMO3 proper)
for phrases and an ‘inner’ composing loop (lines 28-88 of subroutine PHRASE) for notes and rests.
Program DEMO5 proper implements the phrase-composing loop in lines 36-68.
Names of variables and arrays pertaining to phrase attributes adhere to four ‘roots’:
-
PHR— length of phrase. ParameterMPHRfixes the number of phrase lengths at 4 (line 5); lines 13 and 14 populate 4 specific values into arrayVALPHR, populates the corresponding weights from Figure 1 (a) into arrayWGTPHR, and initializes the statistics in arrayCUMPHRto zero. Line 38's call to the library subroutineDECIDEselects a supply valueVALPHR(I)favoring the indicesIfor which the statisticsCUMPHR(I)are smallest.DECIDEplaces this supply value in variableIPHR, then incrementsCUMPHR(I)by1./WGTPHR(I). Because selection of phrase lengths reflects numbers of occurrences and because the largest weight appearing in array WGTPHR is .30, the smallestCUMPHRincrement will be 3.333. The offset used for argument #5 in line 38's call toDECIDEapproximately equals this smallest increment. -
AVG— average note duration. ParameterMAVGfixes the number of average note durations at 3 (line 5); lines 16 and 17 populate 3 specific values into arrayVALAVG, populates the corresponding weights from Figure 1 (b) into arrayWGTAVG, and initializes the statistics in arrayCUMAVGto zero. Line 44's call to the library subroutineDECIDEselects a supply valueVALAVG(I)favoring the indicesIfor which the statisticsCUMAVG(I)are smallest.DECIDEplaces this supply value in variableIPHR, then incrementsCUMAVG(I)byFLOAT(IPHR)/WGTAVG(I). -
ART— articulation within a phrase, expressed as the probability that a rhythmic unit will serve as a rest. ParameterMARTfixes the number of articulations at 4 (line 5); lines 18 and 19 populate 4 specific values into arrayVALART, populates the corresponding weights from Figure 1 (c) into arrayWGTART, and initializes the statistics in arrayCUMARTto zero. Line 46's call to the library subroutineDECIDEselects a supply valueVALART(I)favoring the indicesIfor which the statisticsCUMART(I)are smallest.DECIDEplaces this supply value in variableARTIC, then incrementsCUMART(I)byFLOAT(IPHR)/WGTART(I). -
REG— register within a phrase, expressed as the lowest pitch in a twelve-semitone gamut. ParameterMREGfixes the number of registers at 4 (line 5); lines 20 and 21 populate 4 specific values into arrayVALART, populates the corresponding weights from Figure 1 (d) into arrayWGTREG, and initializes the statistics in arrayCUMREGto zero. Line 48's call to the library subroutineDECIDEselects a supply valueVALREG(I)favoring the indicesIfor which the statisticsCUMREG(I)are smallest.DECIDEplaces this supply value in variableIREG, then incrementsCUMREG(I)byFLOAT(IPHR)/WGTREG(I). -
PRM— primary scale degree for a phrase. ParameterMPRMfixes the number of primary scale degrees at 12 (line 5); lines 22-24 populate 12 specific values into arrayVALPRM, populates the corresponding weights from Figure 1 (e) into arrayWGTPRM, populates the index values 1-12 into arraySCDPRM, and initializes the statistics in arrayCUMPRMto zero. Notice that the contents ofVALPRMare chromatic numbers in circle-of-fifths order. The block of code spanning lines 50-65 select primary scale degrees for phrases.-
First off, line 50 randomly shuffles array
SCDPRMinto random order; this eliminates any bias which might result from how primary scale degrees are enumerated. -
The next step, implemented in lines 51-63, is to identify a primary scale degree
IDXPRMwhich satisfies the provisions listed above and for which the statisticCUMPRM(IDXPRM)is minimal. -
This primary scale degree is saved in variable
IPRM. -
Line 65 increments
CUMPRM(IDXPRM)byFLOAT(IPHR)/WGTPRM(IDXPRM).
-
First off, line 50 randomly shuffles array
Selection of average durations, articulations, and registers all reflect lengths of phrases. Since the shortest phrase length is always
24, while the largest weights stored in arrays WGTAVG and WGTREG are both 1.0, the smallest increment in
DECIDE's line 21 will be 24.0 in each case. The offset of 4.0 used to select average durations and registers
is a sixth of this amount, which produces ‘well-mixed’ choices. The smallest increment for articulations is 24/3, or 8.0,
so articulations are somewhat ‘lumpier’
The phrase-composing loop completes by calling subroutine PHRASE in line 67.
Rhythm
Lines 28-88 if subroutine PHRASE implement the inner loop which composes notes and rests for Demonstration 5.
Choosing to generate a note versus a rest employs the same mechanism used for Demonstration 2,
Demonstration 3, and Demonstration 4.4
Variables and arrays pertaining to note durations have names ending with DUR.
Parameter MDUR fixes the number of durations at 5 (line 2);
lines 10 and 11 populate 5 specific values into array VALDUR, populates the weights depicted in Figure 4 (a)
into array WGTDUR, and initializes the statistics in array CUMDUR to zero.
Durations are selected for notes in line 32 and for rests in line 78. In both instances,
calls to the library subroutine DECIDE select supply values VALPHR(I)
favoring the indices I for which the statistics CUMPHR(I) are smallest. DECIDE
places this supply value in variable DUR, then increments CUMDUR(I) by 1./WGTDUR(I).
The approach is similar to that of Demonstration 3 except that here the repertory of durations is limited to five values
clustered around the average duration.
Since durations are selected with sensitivity to numbers of occurrences and since
the largest weight in array WGTDUR (line 10) is 2.0, the smallest increment for CUMDEG(I) will be 0.5.
The offset used for DECIDE's argument #5 (both line 32 and line 78) is half of this smallest increment.
Lines 33-35 complete note-duration processing by scaling the value returned from DECIDE by AVGDUR, then converting
the scaled duration into discrete sixteenth notes.
Lines 78-81 complete rest-duration processing by scaling the value returned from DECIDE by AVGDUR/2.0, then converting
the scaled duration into discrete sixteenth notes.
Pitches
Line 27 of subroutine PHRASE calls the library subroutine ALIGN
just prior to entering the ‘inner’ composing loop.
This subroutine call insures that degrees shared in common between consecutive scales will retain their cumulative statistics.
PHRASE selects scale degrees for notes using the strategy of the library subroutine DECIDE,
but imposes stylistic constraints upon consecutive intervals.
PHRASE applies these constrains as it computes weights for degrees (lines 55-68); degrees found to violate a constraint receive
null weights. The constraints themselves include a rule forbidding identical degrees for two consecutive notes along with the
stylistic matrix detailed in Figure 5. Information describing this matrix is stored as the 11x11 logical matrix
LGLTVL (lines 13-23 of PHRASE).
Variables and arrays pertaining to scale degrees have names ending with DEG.
Parameter MDEG fixes the number of scale degrees at 7 (line 2);
Line 10 populates 7 specific values into array VALDEG, and initializes the statistics in array CUMDEG
to zero. Notice that VALDEG contains a Lydian scale, expressed as chromatic numbers in circle-of-fifths order.
Each degree is expressed as an offset giving the number of semitones above the primary degree IPRM.
Line 38's call to the library subroutine DECIDE selects a supply value VALDEG(I)
favoring the indices I for which the statistics CUMDEG(I) are smallest. DECIDE
places this supply value in variable IDEG, then increments CUMDEG(I) by 1./WGTDEG(I).
Each scale used in Demonstration 5 is a transposition of the basic form which line 10 of subroutine
PHRASE initializes into array VALDEG.
Lines 50-64 of program DEMO5 select a primary degree in such a manner as to provide equal duration emphasis to each of the twelve primaries, subject to the
constraints described previously.
The block of code spanning lines 36-72 selects a scale degree for a note. Lines 36-59 calculates a weight dynamically for
each scale degree, then lines 60-66 use the methods of the library subroutine SELECT
to accomplish weighted random selection.
If the Ith degree fails to satisfy the constraint matrix shown in Figure 5, then the degree receives a weight of zero.
This determination is made in lines 45-49. The variable LTVL gives the interval between the degree under consideration
and the degree selected for the previous note, while the variable ITVL gives the value of LTVL during the previous
iteration.
DO NOT USE THIS ALGORITHM! If the Ith degree successfully satisfies the constraint matrix shown in
Figure 5, then the degree receives a weight of CMAX-CUMDEG(I)+2.0, where CMAX is the largest
CUMDEG value.4
Selection with Cumulative Feedback
The library subroutine DECIDE5
selects values from a supply, using the method of cumulative feedback to conform selected values to a discrete table of weights.
Calls to DECIDE require seven arguments:
-
RESULT—DECIDEselects a supply value and returns the value in this location. -
VALUE— Supply of values. Duplicate values are not permitted.VALUEmust be an array whose dimension in the calling program isNUM(argument #5 below). -
CUM— Cumulative statistics reflecting how much each supply value has previously been used.CUMmust be a real array whose dimension in the calling program isNUM. Its elements should initially be zero. -
WEIGHT— Relative weights for each value.WEIGHTmust be a real array whose dimension in the calling program isNUM. Each weight must be zero or greater, and at least one weight must be positive. -
OFFSET— Likelihood of selecting the most-used offset.OFFSETmust be real. -
DUR— Duration of item for whichRESULTis being selected.DURmust be a positive real number. -
NUM— Number of supply elements (dimension of arraysVALUE,CUM, andWEIGHTin the calling program).
DO NOT USE THIS ALGORITHM! DECIDE first iterates through the statistics in array CUM,
saving the maximum in the variable CMAX and the total in the variable T.
A chooser value R is calculated as RANF()*(FLOAT(NUM)*(CMAX+OFFSET)-T).
DECIDE next iterates once again through the supply of values.
The iteration for index I, DECIDE calculates W = CMAX-CUM(I)+OFFSET.
If R ≤ W then DECIDE exits from the loop. Otherwise, DECIDE
sets R = R - W and proceeds to the next iteration.
Array element VALUE(I) upon exiting the loop is the supply value which DECIDE
places in RESULT. Just before returning, DECIDE increments CUM(I)
by DUR/WEIGHT(I).
Aligning Diatonic Statistics
The library subroutine ALIGN6
is used to realign statistics in the event of a modulation between diatonic scales. Its purpose is to hand off
statistics both when scale degrees are held in common and where scale degrees are cross-related (e.g. F and F#).
rotate statistics within an array in order to hand off each statistic to the
Calls to ALIGN require five arguments:
-
CUM— Cumulative statistics reflecting how much each scale degree has previously been used.CUMmust be a real array whose dimension in the calling program isNUM. -
IOLD— Old index.IOLDmust be an integer in the range from 1 toMIDX(argument #5 below). -
INEW— New index.INEWmust be an integer in the range from 1 toMIDX. -
MIDX— Maximum index.MIDXmust be a positive integer. IfALIGNis used to map subsets of the chromatic scale or of the circle of fifths, thenMIDXwill be 12. -
NUM— Number of scale degrees (e.g. 7 for a major scale).
Subroutine ALIGN leverages the library subroutine ROTATE
to shift each statistic to the appropriate element of array CUM.
Comments
- The feedback mechanisms employed for these Demonstrations were reworked into the procedures described in “Statistics and Compositional Balance”, where they were rechristened statistical feedback.
- My approach here to cross relations follows that of Arnold Schoenberg in Preliminary Exercises in Counterpoint.
- The weakness of this algorithm is that it allows a supply value to be chosen when the value has already received more than its fair share of usage and when other statistically preferable values exist that also satisfy all constraints.
-
Alternatively, subroutine
PHRASEcould have chosen between notes and rests using cumulative feedback to monitor how often it selected notes versus how often it selected rests. -
The source code for subroutine
DECIDEappears in Automated Composition, Chapter 7, pp. 7-9 to 7-10. Be warned that this source code is bogus. For an effective algorithm, consult “Statistics and Compositional Balance”. -
The source code for subroutine
ALIGNappears in Automated Composition, Chapter 7, pp. 7-17 to 7-18.
| © Charles Ames | Original Text: 1984-11-01 | Page created: 2017-03-12 | Last updated: 2017-03-12 |