Sequence Generation in Java1

Introduction

This topic area of charlesames.net concerns itself with the general topic of sequence generation. Sequence generation includes things like random number generation, chaotic sequence generation, deterministic contours, permutations, Brownian motion, Markov chains, and Chomsky grammars. A necessary adjunct to the topic is the matter of conforming output from generic sequence generators to the precise range needed by a specific application. This may involve remapping continuous sequence values (values with digits right of the decimal point) according to statistical distributions, or it might instead involve using discrete sequence values (values without digits right of the decimal point) as indices for array lookups. In support of the main topic is the topic of control. Sequence generators used in applications are not typically static; they are often required to adjust to some sort of profile that unfolds over time or space.

A sequence generator is a self-contained number-generating algorithm with memory. Each iteration of this algorithm calculates a sample, and does so relative to results obtained during previous iterations. A set of many consecutive samples is called a sequence when the order of samples is significant; it is called a population when order is not relevant.

Order and content are the two most fundamental criteria for evaluating a sequence generator.

Five of the six main sections of this topic delve into order and/or content in one way or another: In Basics I: Randomness, the content portion of the evaluation focuses on how the standard random number generator strives to achieve uniformity over the long term, while the order portion focuses on the independence of samples over the short term. Basics II: Distributions gives a deep dive into content, showing how statistical distributions quantify the overall population of a sequence, abstracting away the order in which samples are presented. Basics III: Permutation likewise gives a deep dive into order by generalizing the means by which values can be drawn from a source set, when some kind of source-set model is being used to generate a sequence. Design I: Driver/Transform presents a design pattern for sequence generation; here an active Driver component takes responsibility for the order of samples while a passive Transform takes responsibility for content. Design II: Index/Supply also describes a design pattern, also with an active order component and a passive content component.

The most iconic of sequence generators is the random number generator. This is where the present treatment starts, and randomness becomes the point of reference against which other sequence generators will be considered. Applications of random sequencing include gaming, digital signal generation (colors of noise), cryptography (one-time pads), politics (jury selection, military drafts), computer-generated landscapes, statistical sampling, random testing in software engineering. These topics explored more fully in the Wikipedia article on "Applications of randomness". I cannot discourse expertly on most of these topics, but I do know something about composing programs, having developed many, having written an unpublished textbook on the subject, and having extracted excerpts from this textbook into an historical survey: "Automated Composition in Retrospect: 1956-1986".

In their innermost loop iterations, composing programs invariably come down to selecting parameters for notes, where a "note" might even be a whack on a snare drum. Such parameters include period between consecutive note onsets, specific note duration, timbre (typically referenced by an integer), loudness, and pitch (sometimes grouped into chords). Approaches to selecting these parameters have historically divided into three categories:

I was Lejaren Hiller's last acolyte, and constrained decision making is the forerunner of what I have done. Much of that includes actions like sorting options in order of preference or like throwing out decisions in the face of impasses and trying alternative solutions. Such actions hardly suit themselves to a sequential pattern. So as much as I personally favor this approach, its relevance to the topic at hand is indirect at best.

The remaining two approaches each suggest generalized design patterns which would allow swapping in alternatives to the random number generator. These alternatives might include different 'flavors' of randomness, chaotically generated sequences, material drawn from nature, or deterministic content.

There has been an additional design consideration influencing all three of the approaches listed previously, and that is the issue of control. Composing programs have often been guided by some sort of profile controlling how the content of a piece unfolds over time; likewise, using sequences to generate graphic images utilizes features such as texture gradients as locations move around the vertical and horizontal axes. So while it may be conceptually simpler to discuss sequence generation out of context, in practice the context generally intervenes.

Randomly Driven Statistical Transforms in the Stochastic Music Program

The Stochastic Music Program exemplifies an approach in which two active driver components drive a variety of passive transforms, which latter take responsibility for the range of parameter choices and are how choices are distributed within this range. This is the approach explored under the topic Design I: Driver/Transform.

The synopsis which follows is drawn both from Xenakis's book, Formalized Music5, and by a lecture given to our 1979 computer composition class by John Myhill based upon Myhill's own analysis of Xenakis's FORTRAN code.6 (I have not read through Xenakis's program myself.)

The more prominent driver component is the standard random number generator, which evenly (equal numbers of values in equal-sized regions, over time) spreads driver values over the domain from zero to unity. A second driver component is a flavor of randomness developed (according to Myhill) by Émile Borel. This process still produces values in the domain from zero to unity, but it damps down transitions between consecutive samples, favoring smaller steps over larger leaps.

The Stochastic Music Program has two levels of organization. An outer loop chooses parameters like duration and density for sections. An inner loop chooses parameters like start time, timbre number, duration, pitch, and dynamic for notes. Since parameters at both levels follow varied distributions it is revealing to detail which distributions apply to which parameters. Do not take this as an exhaustive description of how the program operates or what influenced Xenakis to do what he did.

Outer Loop: Sections

Each musical section generated by the Stochastic Music Program is characterized by its duration, how long it lasts, and its density, how many notes it contains.

Section durations behave as an outer Poisson Point Process, which is a scenario developed by probability theory to model experiences like waiting for a fish (poisson) to bite or like waiting for an unstable atom to eject a beta particle. The waiting-time distribution in its pure form is called "negative exponential" or, more simply, "exponential". The control parameter for selecting section durations is the average section time.

To select section densities, Xenakis's program uses Borel's process to generate a driver value, then scales this value to the range from 0 to 6. The section density directly influence the periods spent waiting between note onsets; it also indirectly influence the selection of timbres (string instruments can produce four timbres: col legno, pizzicato, tremolo, or glissando) for notes.

Xenakis created piecewise linear functions such as the ones for "ST-10" graphed in Figure V-2 of Formalized Music (p. 139) or the ones for "ST-4" graphed in Figure 8 of Automated Composition in Retrospect (p. 175). Each function Wk(d) maps a section density d to the likelihood of selecting timbre k. (One function for each value of k.) At the beginning of each section, these functions were unpacked into an array of timbre-likelihoods which Xenakis described as the (momentary) "Composition of the Orchestra".

Inner Loop: Notes

The period of time between consecutive note onsets behaves as an inner Poisson Point Process with a much shorter average duration than for sections. This control parameter is in fact the inverse of the section density. Thus dense sections will have shorter note-to-note periods and sparse sections will have longer note-to-note periods.

Timbres were selected randomly according to the array of timbre-likelihoods assembled at the beginning of each section.

Durations for individual notes follow a truncated Gaussian or Normal Distribution, the familiar bell curve from statistics. Each instrument is assigned a maximum duration based on, for example, the longest note that a string instrument player can practically sound at volume with one draw of the bow, or the longest note a wind instrument player can readily sound in one breath. The peak of the bell curve is situated above the mid point, 1/2 the maximum duration, and horizontal scale is ajusted so that a note duration of zero corresponds to 4.25 standard deviations below the mid point while the maximum duration corresponds to 4.25 standard deviations above the mid point.

The Stochastic Music Program conditioned pitch selection for individual notes upon the previous pitch played by the same instrument using a process equivalent to requesting output from a Borel driver and scaling the Borel output to the instrument's range. If the note is a gliss, the rate of glissando follows a Gaussian/Normal (bell) curve, with static pitch at the center of the hump, with slow glisses in the high probability slopes, and rapid glisses in the low probability tails. (So Xenakis asserts in his book, though John Myhill suggested there might be a bug.)

The Stochastic Music Program was used by Xenakis to generate multiple pieces, each differing from one another in the size and membership of the ensemble. The only aspect of continuous control was not time-based, but rather in the piecewise continuous graphs mapping the section density (a single number) to an array of timbre probabilities.

Each run of the Stochastic Music Program produces a score with a sectional form, a rhythmic style emulating beta decay, and a pan-chromatic pitch usage. Although it accepts end-user data input, the data is specifically limited to a mapping from how active a section is (notes per second) to the proportions of timbres selected, along with details of timbre capabilities (for example, pizz. notes have short durations while glissandi have long durations). It could therefore be argued that all scores produced by the Stochastic Music Program were 'composed' by Xenakis, and that anyone else employing the program could at best claim the role of 'arranger'.

Indexed Selection from Supplies in Project2

Gottfried Michael Koenig's Project2 exemplifies an approach in which an active index generator (Koenig calls this a "selection principle") is used to dereference a note-parameter value from a passive array or collection (which Koenig calls a "supply"). This is the approach explored under the topic Design II: Index/Supply.

Project2 was created by Gottfried Michael Koenig as a utility which he (the programmer) and his students (mostly non-programmers) could use to generate compositions. Like the Stochastic Music Program (and all other composing programs), the operation of Project2 ultimately comes down to selecting parameters for notes. By contrast to the Stochastic Music Program, Project2 does not prescribe specific distributions for parameters. Neither does Project2 fix the standard random number generator (or in a few hard-coded instances, the Borel process) as the active component of the parameter-selection process. Rather, users of Project2 provide "supplies" (within which a distribution is inherent) and specify "selection principles" to draw elements from these supplies.

Koenig's notion of selecting from a "supply" corresponds exactly to the urn model of Jacob Bernoulli. The urn-model act of blind "selection with replacement" is implemented by the ALEA principle, which chooses supply elements using a uniform random index. The urn-model act of "selection without replacement" is implemented by the SERIES and SEQUENCE principles. SERIES implements blind selection by iterating its members in shuffled order. SEQUENCE implements non-blind selection by iterating its members in their original user-specified order.

Project2's features are too numerous to cover here, but details may be found in the Project2 technical manual.


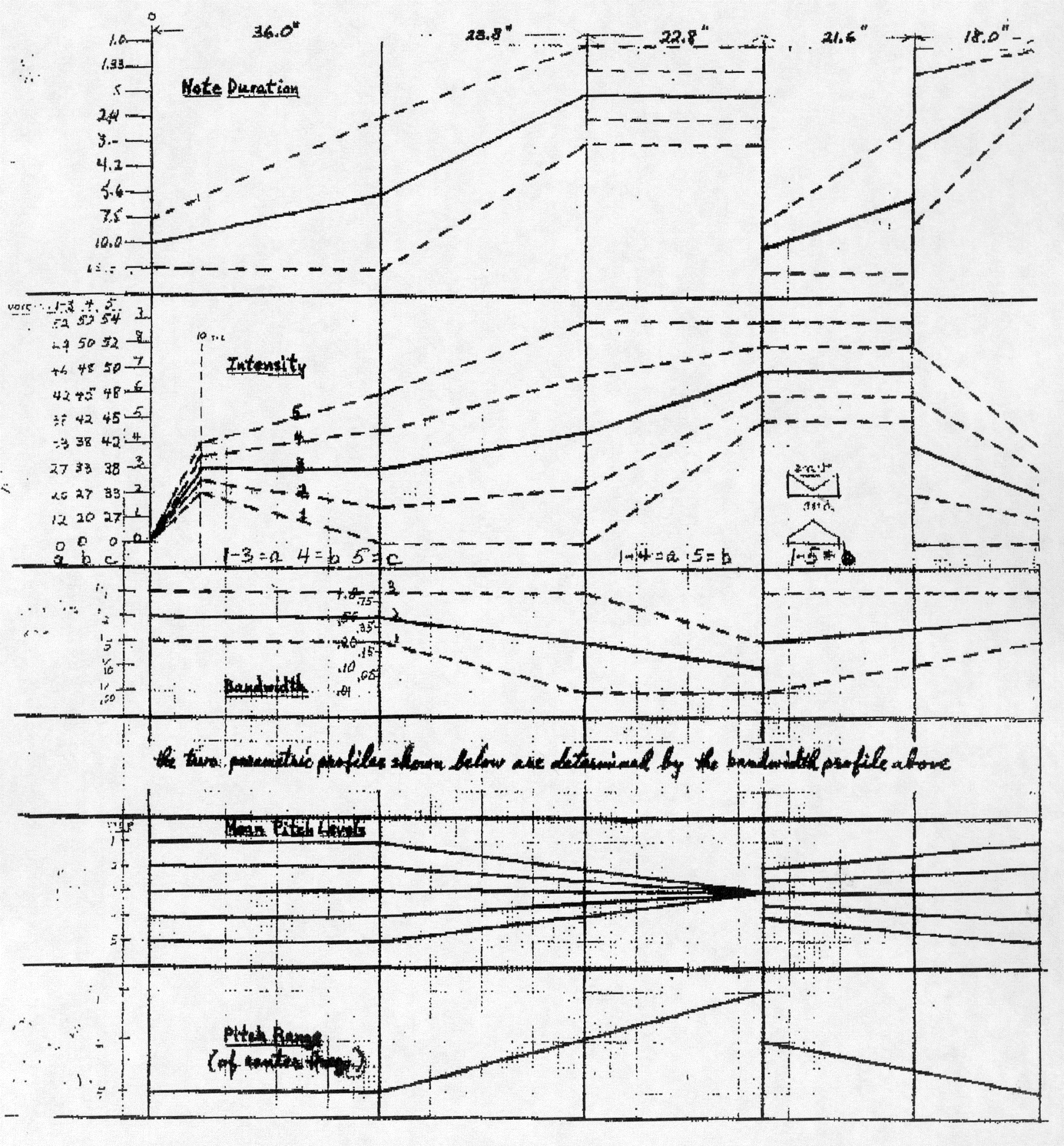
Figure 1: Parametric means and ranges for James Tenney's 1961 Noise Study. Reproduced from (Tenney, 1969).

Control Over Time

Xenakis's work has influenced several composers who have developed composing programs of their own. These programs are distinguished from Xenakis in that they impose direct time-based control over the distributions which in turn guide the selection of note parameters. This is the approach explored under the topic Design III: Contours.

Earliest among these composers was James Tenney, whose 1961 "Noise Study" in fact predated the Stochastic Music Program. (Nonetheless the chain of influence was from Xenakis to Tenney, who was fully aware of the statistical procedures Xenakis employed on paper to create Xenakis's 1957 composition "Achorripsis".) The profile of Tenney's "Noise Study"5 was determined by the graphs reproduced here as Figure 1.

Other notable examples of time-based control include Thomas DeLio's 1976 "Serenade" 6 and John Myhill's 1985 "Toy Harmonium" 7

Topic Overview

This topic area on sequence generation has five main subjects:

Coding

I am employing the term package consumer to indicate the targeted reader of this topic area: a developer who wants to deploy this functionality within a larger project. The package consumer is thus distinguished from the end user who hopefully will be enjoying the fruits of the developer's efforts.

Why Java?

This is a practical guide to sequence generation and as such is enriched by actual code examples. The programming language is Java. I am not a language partisan; in the past I have attempted language neutrality by describing algorithms in English. This was a mistake, which I discovered when using this published material to reconstruct my own code. Providing examples in actual language allows both syntax checking and testing for effective functionality.

Why Java specifically? Attractive features of Java include:

Syntax

Familiarity with Java syntax is assumed in these pages. I have taken a cue from the Eclipse IDE, which I use, and colored the code examples to distinguish symbol types. The coloring rules are explained in Table 1.

Symbol TypeColorExamples
KeywordBrown   for (int i = 0; i < 5; i++) {
VariableYellow   boolean flag = MyClass.getFlag();
Object TypeDarkBlueclass MyClass {
enum Category {
interface Client {
FieldTurquoise   int counter;
MethodGreen   System.exit();
Method
Parameter		Purple    MyClass.setFlag(boolean flag) {
Generic
Parameter		Fuchsia class GenericClass<T> extends Object {
   T value;
   void setValue(T value) {this.value = value;}
   T getValue() {return value}
Table 1: Coloring rules for Java code examples.

Design Patterns

Pedagogically, the next step after learning the syntax of a language is to see it applied to challenges commonly faced by programmers. This is partly what the Design Patterns movement is about. It had been my intention the present pages would contextualize my particular implementations within the larger framework of design patterns but (to borrow a phrase from Karl Kohn with respect to a widely regarded musical-theory text), "the more I read it, the less I understand it". The one pattern I get unequivocally is the singleton pattern. I seem to favor most the composite pattern, since the great majority of my object structures have whole-and-parts relationships.

Two design patterns are featured in this presentation which originate outside the design-pattern community. The first design pattern is Driver/Transform, which abstracts the approach described above for the Stochastic Music Program. The second design pattern is Index/Supply, which abstracts the approach taken in Project2.

Persistence

Persistance is very important when you're working with unpredictable sequence data. If the data is unpredictable, that means that different runs will produce different outcomes. Its nice to be able to consider several alternative outcomes and choose the one that best suits. That means keeping stuff around long enough to make a choice.

I have included no persistence methods in my code examples, but be assured every class presented in this topic area originally did have a persistance component — I just cut that part out when converting the code into HTML. For the record, I don't directly do any text-stream parsing or formatting. Instead, I use Java's implementation of the XML Document Object Model platform. This platform supports parsing an XML-formatted text stream into a hierarchy of org.w3c.dom.Node instances (the "model"), and the platform also supports serializing a Node hierarchy into a character stream. This is useful, not just for file I/O, but also for copying child objects along with their own dependents from one composite structure to another (e.g. via a text Clipboard).

In addition to the mechanics of converting from Java object to XML nodes and back, my code is also responsible for generating an XML Schema, eliminating the error-inviting chore of maintaining such a schema manually. Only a subset of possible XML designs comply with what XML Schemas will tolerate, but once I got used to defining a unique node name for each instantiatable class, XML-Schema compliant designs have served my purposes perfectly.

Comments in Code

Comments in code are deprecated as a code smell, but as an aging programmer with a great pileup of code, I have struggled all too often to figure out what any portion of this code does after I've left it for a while. My comprimise is Javadoc. Javadoc encourages me to explain classes, their properties and methods, and other things in a systematic way. It also produces an elegantly formatted and cross-linked HTML document which, if done right, explains how all my code units work together.

You can distinguish a Javadoc comment from a regular block comment because the Javadoc comment starts off with two asterisks (/**) while a regular block comment starts with just one (/*). Javadoc commentary is also structured using tags like @param, @return, and @throws for methods.

Javadoc doesn't recognize properties, which are generic to OO and only implicit to Java. Java does implement all the components of a property: a field to hold data within the scope of the object itself, and two methods to access field data externally. The method that transfers data from an external actor into a field is called the setter, while the method that transfers data out of the fields to an external actor is called the getter. Most readers already know these things. The challenge here is how Javadoc should tie them together. Well it turns out that when one javadocs a field, that field description gets published even when the field itself is private. So when I document the getter, I don't need to explain the purpose of the field, or to specify the field's range — that stuff applies directly to the field. Instead I state briefly that the method is a getter and provide a @link to the field. Javadoc does the rest. Likewise for setters.

Listing 1 mocks up a code example showing how I use Javadoc to document a property. I have not seen other programmers using this approach (at least nothing showed up on StackOverflow).

/**
* Mock class to illustrate how I document properties in Java.
* @author Charles Ames
*/
class ObjectWithIndexProperty {
   /**
   * Stores the position of a data item in an array or collection.
   * Ranges from 0 upwards.
   */
   int index = Integer.MIN_VALUE;
   /**
   * Getter for {@link #index} field.
   * @return The assigned {@link #index} value.
   * @throws UnsupportedOperationException when {@link #index} field has not been initialized.
   */
   int getIndex() {
      if (Integer.MIN_VALUE == index)
         throw new UnsupportedOperationException("Index not initialized");
      return index;
   }
   /**
   * Setter for {@link #index} field.
   * @param The intended {@link #index} value.
   * @throws IllegalArgumentException when the argument is negative.
   */
   void setIndex(int index) {
      if (0 > index)
         throw new IllegalArgumentException("Index cannot be negative");
      this.index = index;
   }
}
Listing 1: How I document an object property by linking field, getter, and setter through Javadoc.

Backstory

Course & Book

During this first year the topic of digital sound synthesis was handled by me, while the topic of computer composition was handled by John Myhill (with guest lectures by Lejaren Hiller). Several of Myhill's lectures focused on Xenakis's Stochastic Music Program, on existing statistical methods which Xenakis had made use of, and on Myhill's own simplifications and improvements to Xenakis's program. In later years the sound-synthesis component of the course dropped away (we no longer had a functioning DAC) and I took over the computer-composition topic. For the subtopic of statistical generation, my approach had evolved from Myhill's. It was not my goal to teach students how to recreate Xenakis's program but rather give them a generalized toolset that would allow them to adapt Xenakis's approach to their own needs.

When I set about building a toolset, it had become clear that students would gain most flexibility if separating the (active) sequence-generating components from the (passive) distribution-mapping components became a policy. The number of options would increase to the number of sequence-generator types times the number of distributions. To ensure compatibility between these two components I imposed two requirements on the toolset:

The most urgent need on the driver side was to gather together a rich selection of processes. This activity is documented in my Catalog of Sequence Generators.

Since the chaotic drivers Logistic and Baker generate very recognizable motivic shapes, I devised the Fracture component to enrich their possibilities. Fracture divides the driver range into equal-sized regions; it then uses a randomly shuffled permutation to relocate values from one region to another. Fracturing makes sense when values concentrate around strong attractors, but it makes less sense for other driver categories. Fracturing was originally described in my Catalog of Statistical Distributions.

One more innovation was the Level component, which I first described in How to Level a Driver Sequence.

Comments

  1. This topic area of charlesames.net consolidates material from articles originally published in Leonardo and Leonardo Music Journal during the 1980's.
  2. The mechanics of creating the "Illiac Suite" are explained in the 1959 book Experimental Music.
  3. Xenakis's Stochastic Music Program is described in chapter 5, "Free Stochastic Music", of his 1971 book Formalized Music: Thought and Mathematics in Composition, pp. 131-154. A FORTRAN listing of the program is included on pp. 145-152. At the 1978 ICMC, which Xenakis also attended, John Myhill proposed "Some Simplifications and Improvements in the Stochastic Music Program", which presentation initially raised some ire on Xenakis's part.
  4. Koenig's Project2 program is described in the 1971 article Project2: A programme for musical composition.
  5. Iannis Xenakis's book was presented to me by my high-school music teacher during the early 1970's. The book both perplexed and intrigued me. It was partly my desire to figure it out that led me to double major in music and mathematics as an undergraduate at Pomona College. Many of my courses were selected with a mind toward better understanding Formalized Music; for example: Electronic Music, Probability and Statistics, Stochastic Processes, Abstract Algebra. I also sought out people capable of explaining Xenakis's book to me. My first tutor was Ted Chinberg, then a mathematics major at Harvey Mudd College and also a drummer in jazz groups where I played trumpet.
  6. John Myhill was Professor of Mathematics at the State University of New York at Buffalo, where I arrived in 1977 to pursue graduate studies in musical composition. He was close friends with Lejaren Hiller and a great fan of Iannis Xenakis. One of my most hilarious memories was John Myhill flowcharting Xenakis's Stochastic Music Program (a long vertical list of steps) from memory across a wide set of chalkboards. For each musical attribute (timing, instrument choice, note duration, pitch, dynamic, etc.) he identified the statistical distribution applied, drew a density graph, and described the underlying scenario.
  7. The "Noise Study" was one of several projects Tenney worked on during a residency at Bell Labs. This and other compositional projects are described in his 1969 account, Computer Music Experiences, 1961-1964. There was also a Computer Study of Violin Tones.
  8. A description of procedures used to create DeLio's "Serenade", including a score excerpt, appears on pp. 179-181 of Automated Composition in Retrospect: 1956-1986.
  9. The contours for "Toy Harmonium" are reproduced in Automated Composition: An Installation at the 1985 International Exposition in Tsukuba, Japan, p. 201. A sound recording is included in this site's description of the 1985 Tsukuba Installation.

© Charles Ames Page created: 2022-08-29 Last updated: 2022-08-29