Speech Synthesis:
Conclusions

I began this exercise knowing much less than I thought about speech synthesis. Here's what I learned:

Diversity of Speech Sounds

The diversity of speech sounds is huge, and how a phoneme unfolds can depend upon both where the phoneme is situated within a word and what other phonemes surround it. The practical exercise of synthesizing “Daisy Bell” has taken us through all of the phoneme categories employed by English, and practically all of the phoneme instances. However the sounds of English are a small subset of the sounds employed by languages worldwide. We have seen, for example that the English nasals are just three of sixteen nasal consonants recognized by the International Phonetic Alphabet. And there is at least one phoneme category not used by English at all: click consonants.

Enhancements to the MUSIC-N Note-List Model

The note-list model of historical MUSIC-N sound-synthesis engines is inadequate for speech synthesis. This exercise in speech synthesis demonstrated two ways in which the note-list model falls short, but also implemented fixes for each shortcoming. These fixes, in turn have implications reaching far beyond speech synthesis.

Ramps

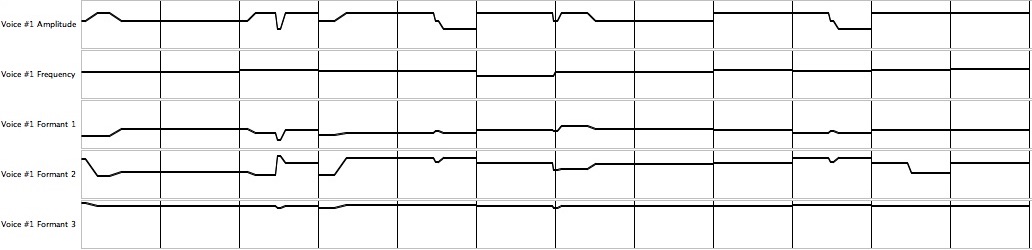
Figure 5: Graph of contours for the sixth-iteration synthesis of “Daisy Bell”. Time range from 72.00 to 84.00 seconds.

To integrate speech synthesis into musical synthesis it is not enough to supply discrete note-by-note parameters, but it is also too much to specify an array of values for each 5-msec slice of time (this is what the Klatt speech synthesizer requires). The happy compromise implemented here was ramped control signals. These signals are built up from segments which interpolate continuously from an origin to a goal, and their great advantage is that the number of segments can vary dynamically from word to word.

Figure 5 was produced by the Note List Editor working on Listing 8, the sixth-iteration synthesis of “Daisy Bell”. It graphs the contours for the lyrics, “… you'll look sweet, upon the seat of a …”. The duration scale is linear (seconds), while the amplitude scale (cents) and frequency scales (decibels) are logarithmic. This contour-graphing tool helped me identify and repair several anomalies, taking advantage that of the fact that discontinuities should not occur in the midst of a sound — not unless one actually desires to produce a click. This consideration applies both to primary discontinuities such as amplitude spikes and to secondary discontinuities such as instantaneous frequency changes.

Modules

A second requirement for speech synthesis is that sounds need to be processed in a modular way. This happens for example with nasals where sounds processed by Instrument #121: Mouth1 were additionally processed by Instrument #122: Nose1.

Rerouting vocal sounds through the nose is acoustically similar to muting a violin bridge or covering a trumpet bell with a toilet plunger. And the analogy goes even farther. Think for example of the phenomenon of sympathetic resonance built into instruments like the sitar and the hurdy-gurdy, or coaxed from the piano by Schoenberg in the “flageolet” tones of Opus 11, Number 1. Such resonances can be emulated synthetically using audio-frequency comb filters, and they can be invoked modularly by passing voice-level signals between notes. From here it is only a small generalization to reverberation effects being applied selectively to specific passages within a synthetic rendition.

K1# Q$3 Q=60
M1 H. deɪ D5/
M2 H. zi ~B4/
M3 H. deɪ G4/
M4 H zi ~D4 QR/
M5 Q gɪv E4 mi F jər G/
M6 H æn E4 Q sər ~G/
M7 H. du D4/
M8 H &D4 QR/
M9 H. aɪm D5/
M10 H. hæf B4/
M11 H. kreɪ G4/
M12 H zi ~D4 Q ənd F#/
M13 Q ɔl E4 fər F ðə G/
M14 H ləv A4  Q əv B/
M15 H. ju A4/
M16 Q &A4 R ɪt B/
M17 Q woʊnt C5 bi B4 ə A/
M18 H staɪ D5 Q lɪ∫ ~B4/
M19 Q me A4 H rɪdʒ ~G/
M20 H &G4 Q aɪ A/
M21 H kænt B4 Q ə G/
M22 H fɔrd E4 Q ə G/
M23 Q ke E4 H rɪʒ ~D/
M24 Q &D4 R bət D/
M25 H jul G4 Q lʊk B4/
M26 Q swit A4 R ə D/
M27 H pɔn ~G4 Q ðə B4/
M28 Q sit A4 əv B ə C5/
M29 Q baɪ D5 sɪ ~B4 kəl ~G/
M30 H bɪlt A4 Q fər D/
M31 H. tu G4/
M32 Q &G4 H R/
Z

Note-List Explosion

Note-lists are examples of a delimiter-separated file format. As file formats go, delimiter-separated formats are fairly character efficient. XML, by comparison, can balloon file sizes out by factors as large as ten. Still, it ultimately took quite a bit of text to encode the melody and phonemes of “Daisy Bell” as a note list.

For example the number of statements to synthesize the word “can't” at time 60.00 exploded from 4 when just pitch and rhythm were being accommodated (Listing 2) to 66 (over 16×) when all phonemes were included (Listing 8). The overall notelist size increased from 359 lines in Listing 2 to 1684 lines (almost 5×) in Listing 8. Such statement volumes go well beyond the point of impracticability for direct notelist preparation. Stated baldly, producing notelists to synthesize speech sounds, or — for that matter, sounds of comparable intricacy — takes a program.

Listing 9 illustrates a highly character-efficient preparation which might provide input for such a program. This preparation melds the IPA encoding originally presented in Listing 3 into Alan Ashton's linear music code.

For the record, my own effort did not implement a solution as prosaic as parsing Listing 9. That would have required knowing what I was doing ahead of time, when I was actually learning as I went. My code looked more like Listing 10, except that the actual code was interspersed with conditional blocks to adapt results to each synthesis iteration.

Yet the practical knowledge gained while undertaking this exercise could ultimately have been codified into rules for converting IPA symbols into note and ramp statements. Of course computer keyboards don't have the facility to shift into green, and the ASCII character set doesn't recognize symbols such as ∫ or ʒ. The rules would need to mandate timings for terminal consonants, like the v at the end of “give” (measure 5), and one would need to know what to do with words like “won't”, (measure 17) where the nominal durations of a glide, a diphthong, and a nasal together extend out too long to locate the terminating plosive t on the upbeat eighth.

noteList.createCommentStatement("won't");
noteList.createRampStatement(1, 2, time, QUARTER, 261.6, 261.6, "C4");
setFormantTime(time);
createFormantRamps(noteList, 0.05, Approximant.W, Approximant.W);
createFormantRamps(noteList, 0.07, Approximant.W, Vowel.OE);
createFormantRamps(noteList, 0.08, Vowel.OE, Vowel.SHORT_OO);
createFormantRamps(noteList, 0.05, Vowel.SHORT_OO, Nasal.N);
createFormantRamps(noteList, EIGHTH-0.29, Nasal.N, Nasal.N);
createFormantRamps(noteList, 0.02, Nasal.N, Plosive.T);
createFormantRamps(noteList, 0.02, Plosive.T, Plosive.T);

createFormantRamps(noteList, 0.02, Plosive.T, Plosive.T);
createFormantRamps(noteList, 0.06, Plosive.T, MID_AMP, Vowel.IH, LOW_AMP);
createFormantRamps(noteList, EIGHTH-0.08, Vowel.IH, LOW_AMP, Vowel.IH, LOW_AMP);

createBuzzNote(orchestra, noteList, time, EIGHTH, 0.03, false);
Plosive.T.createBurstNotes(orchestra, noteList, time+EIGHTH, .2);
createWhisperNote(orchestra, noteList, time+EIGHTH, 0.2, .02);
noteList.createNoteStatement(new double[]{noteList.nextNoteID(), 1, 119, 0, time, EIGHTH+0.2},
    orchestra.getInstrument(119).getName());
noteList.createNoteStatement(new double[]{noteList.nextNoteID(), 1, 121, 0, time, EIGHTH+0.2},
    orchestra.getInstrument(121).getName());
noteList.createNoteStatement(new double[]{noteList.nextNoteID(), 1, 122, 0, time+0.20, 0.28, 0.05, 0.02,
    Nasal.N.getNotchFrequency(), Nasal.N.getNotchBandwidth(), Nasal.N.getGain()},
    orchestra.getInstrument(122).getName());
noteList.createNoteStatement(new double[]{noteList.nextNoteID(), 1, 199, 0, time, QUARTER-OVERLAP},
    orchestra.getInstrument(199).getName());

Transition Timing

The encoding in Listing 9 masks a tension between explicit melodic durations and phoneme transition timings, which are implicit in conversion rules. This tension exists because the linear music code expresses rhythmic durations relatively, in fractions of a quarter note which themselves depend upon a tempo contour. By contrast, the phoneme conversion rules express transition timings absolutely, in milliseconds. (What I here refer to as “relative time” is the same as what Rogers and Rockstroh refer to as “score time”.)

More specifically, plosives transition over around 50 msec.; glides transition over around 100 msec.; while diphthongs transition over around 300 msec. Such transition timings are by no means hard and fast. I am no phonologist, but I suspect that English speakers from the American South linger upon diphthongs longer than do their Northern compatriots.

While timings may well vary with dialect, they most emphatically do not vary with rhythm. Well, mostly not. Consider the word “won't” at time 48.00 in Listing 8. Here an eighth-note duration (500 msec.) is just too short to accommodate a glide (100 msec.), a diphthong (300 msec.), an on-glide into a nasal (100+ msec.), a nasal steady-state (100+msec.), and a set-up transition for the plosive t (20 msec.). However as note durations stretch out, plosive transitions stay fixed, while glides and diphthongs stretch only up to a limit. Beyond that all of the slack is taken up by phoneme steady-states.

Transition timings are likewise unaffected by tempo, at least up to the point where word durations begin encroaching upon transition durations. “Daisy Bell” has been realized at ♩=60 simply for the purpose of producing readable note lists. However, ♩=180 (0.33 sec/qtr) is a more reasonable Tempo di Valse. At the slower tempo, the word “your” (time 14.00 in Listing 8) encodes j as a 50-msec. steady state (as the amplitude ramps up from silence) followed by a 150-msec. transition into ə. The neutral vowel holds steady for another 150 msec., then transitions over a third 150-msec. segment into r. This third phoneme extends out for the remainder of the quarter (500 msec). At the faster tempo, these phonemic evolutions would need to be compressed down into 333 msec. Most of the excised time would come from the final r. A likely candidate for excision after r would be the steady-state phase for ə.

Absolute milliseconds are also the appropriate time unit for the phases of amplitude envelopes. Encoding these timings is less problematic because timings for characteristics such as attack duration, hold duration, and decay rate, and release time are generally processed discretely by the envelope generator — you send these facts over at the beginning of the note, and the generator works out for itself how long each envelope phase should last. The exceptional phase is the period of silence between consecutive notes. The synthesis examples documented at the link demonstrate that the spacing which most strongly accents the to note of a consecutive pair is around 80 msec. This timing is not affected by rhythm or tempo.